Geometri: Pengertian, Cabang Ilmu, Rumus, Soal
Pada kesempatan ini, kita akan bahas sesuatu yang pastinya sudah sangat familiar dalam kamus kehidupan kita yaitu geometri.
Pengertian Geometri
Geometri merupakan salah satu cabang dari matematika yang fokus pada pengukuran, pernyataan terkait bentuk, posisi relatif sebuah gambar, pandang ruang, dan lain sebagainya.
Pada bangku sekolah, kita belajar bahwa geometri terbagi menjadi dimensi satu, dua, dan tiga.
Selanjutnya akan kita bahas secara singkat mengenai geometri hanya pada dimensi satu dan dua saja.
Geometri Dimensi 1
Pada dimensi satu, kita akan menemukan titik dan garis. Titik adalah sesuatu yang memiliki posisi namun tidak memiliki ukuran entah itu luas maupun volume.
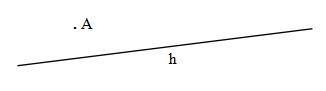
Dalam matematika, titik ditandai dengan huruf kapital. Sedangkan garis ialah kumpulan dari titik-titik yang berderet sampai pada jarak tak hingga, dan untuk membentuk sebuah garis diperlukan minimal dua titik yang dapat tarik garis lurus dari salah satu titik ke titik yang lainnya.
Garis tidak memiliki luas maupun volume, namun ia dapat dihitung panjangnya. Dalam bahasa matematika, sebuag garis dilambangkan dengan huruf kecil. Di bawah ini merupakan gambar dari titik dan garis:
Geometri Dimensi 2
Selanjutnya akan kita bahas geometri dimensi dua secara umum.
Seperti yang kita ketahui pahwa dimensi dua berbentuk bidang datar, sehingga pada dimensi dua tentunya akan kita bahas hal-hal terkait bentuk bangun datar yang terdapat pada dimensi dua.
Berbeda dengan dimensi satu, bangun datar pada dimensi dua memiliki ukuran berupa panjang, luas, dan keliling.
Bangun datar yang biasanya dibahas pada lingkup dimensi dua antara lain segitiga, persegi, persegi panjang, jajar genjang, trapesium, layang-layang, belah ketupat, dan lingkaran.
1. Segitiga
Pertama adalah segitiga, yang mana dapat dibentuk dengan menghubungkan tiga titik pada bidang yang sama dengan syarat bidang tersebut tidak sejajar.
Jenis-jenis segitiga antara lain segitiga sama sisi, segitiga sama kaki, dan segitiga siku-siku. Di bawah ini adalah tabel dari segitiga-segitiga tersebut:
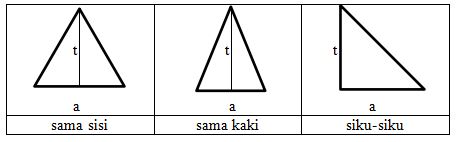
Segitiga sama sisi adalah sebuah segitiga yang memiliki sisi yang sama panjang dan ketiga sudutnya sama besar.
Segitiga sama kaki adalah sebuah segitiga yang memiliki dua sisi yang sama panjang dan dua sudut yang sama besar.
Sedangkan segitiga siku-siku adalah sebuah segitiga yang salah satu sudutnya adalah sudut siku-siku.
Selain ketiga jenis segitiga yang sudah disebutkan, terdapat pula segitiga sebarang yang ketiga sisinya tidak ada yang sama panjang dan ketiga sudutnya tidak sama besar.
Lalu, dalam penghitungan luasnya dapat menggunakan rumus:
L = ½ a × t
dengan
- L = luas segitiga
- a = alas segitiga
- t = tinggi segitiga.
2. Persegi
Merupakan sebuah bangun datar yang memiliki 4 sisi yang sama panjang dan 4 sudut yang sama besar (siku-siku). Gambar persegi adalah sebagai berikut:
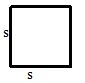
dengan rumus luasnya yaitu:
L = s2
dan rumus kelilingnya yaitu:
K = 4s
dengan s = panjang sisi.
3. Segi Enam Beraturan
Seperti yang sudah dijelaskan di atas terkait segi enam beraturan bahwa segi enam beraturan memiliki 6 sisi yang sama panjang dan 6 sudut yang sama besar.
Berikut penjelasannya dalam bentuk gambar:
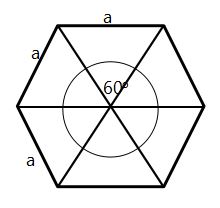
Perhatikan gambar di atas. Dapat kita ketahui bahwa bangun datar segi enam beraturan terbentuk dari 6 buah segitiga sama sisi.
Hal itu dapat dibuktikan jika kita membagi sudut pusat yang mana sebesar 360o menjadi 6 buah sudut yang sama besar, maka didapatkan angka 60o.
Selanjutnya, dapat kita pastikan bahwa sisi yang membentuk sudut 60o sama panjang, sehingga dua sudut lain yang terbentuk adalah 60o pula.
Hal itulah yang membuat segitiga tersebut adalah segitiga sama sisi yang mana memiliki panjang sisi yang sama yaitu a satuan panjang.
Rumus Luas Segi Enam Beraturan
Setelah memahami bangun segi enam beraturan secara bentuk dan asalnya, sekarang kita akan membahas rumus mencari luas segi enam beraturan. Rumus luas segi enam beraturan berasal dari jumlah luas segitiga sama sisi dengan panjang sisi a satuan panjang seperti di bawah ini:
L = 6 x luas segitiga sama sisi
= 6 (½×a×a×sin 60o)
= 6 (½×a2×½√3)
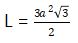
Contoh Soal Segi Enam
Carilah panjang sisi dari sebuah segi enam beraturan dengan luas 100 cm2!
Jawab:

Kita telah membahas banyak tentang bangun datar segi enam. Selanjutnya, seperti yang kita ketahui bahwa semua bangun datar pasti memiliki bentuk limas maupun prisma. Selanjutnya kan kita bahas mengenai prisma segi enam.
Prisma Segi Enam
Prisma segi enam beraturan merupakan sebuah bangun ruang prisma yang memiliki alas dan tutup berbentuk segi enam beraturan.
Bentuk bangun prisma segi enam beraturan beserta rumus menghitung volumenya adalah sebagai berikut:
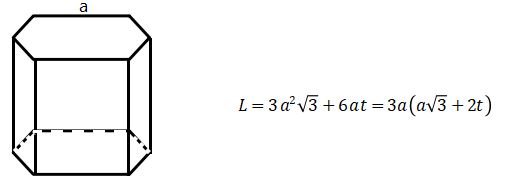
Dengan V = volume prisma dan t = tinggi prisma, atau secara umum dapat kita katakan bahwa volume prisma adalah luas alas dikalikan dengan tinggi prisma.
Sedangkan luas permukaan prisma segi enam merupakan hasil penjumlahan semua sisi dari prisma segi enam beraturan.
Limas Segi Enam
Berbeda dengan prisma, limas segi enam merupakan sebuah bangun ruang dengan alas berbentuk segi enam dan puncaknya merupakan sebuah titik sudut atau mirip sebuah piramida dengan alas segi enam beraturan.
Berikut adalah bentuk berikut volume dan luas permukaannya:
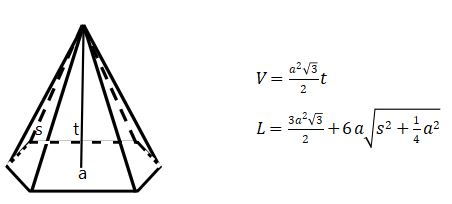
dengan V = volume limas, s = sisi tegak, dan t = tinggi limas, atau secara umum dapat kita katakan bahwa volume limas adalah dikalikan dengan luas alas dan tinggi limas.
Sedangkan luas permukaan luas limas segi enam adalah luas alas ditambah enam kali luas segitiga tegak seperti yang tercantum di atas.
Contoh Soal Prisma dan Limas Segi Enam
Cari volume dari prisma dan limas segi enam beraturan yang panjang sisi alasnya adalah 2 cm dan tingginya 3 cm!
Jawab:
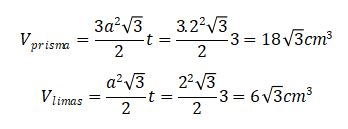
Merupakan sebuah bangun datar dengan 2 pasang sisi yang berhadapan sama panjang dan 4 sudut yang sama besar. Gambar persegi panjang adalah sebagai berikut:
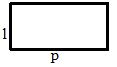
dengan rumus luasnya yaitu:
L = p × l
dan rumus kelilingnya yaitu:
K = 2(p + l)
dengan
- p = panjang
- l = lebar.
Pelajari lebih lanjut Persegi Panjang.
4. Jajar genjang
Merupakan sebuah bangun datar dengan 2 pasang sisi yang berhadapan sama panjang dan 2 pasang sudut yang berhadapan sama besar.
Gambar jajar genjang adalah sebagai berikut:
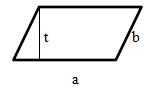
dengan rumus luasnya yaitu:
L = a× t
dan rumus kelilingnya yaitu:
K = 2(a + b)
dengan
- a = alas
- b = panjang sisi miring
- t = tinggi.
Pelajari lebih lanjut di Jajar Genjang.
5. Trapesium
Merupakan sebuah bangun datar dengan 2 pasang sisi yang berhadapan. Gambar trapesium adalah sebagai berikut:
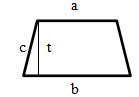
dengan rumus luasnya yaitu:
L = ½ (a+b) × t
dan rumus kelilingnya yaitu:
K = a + b + 2c
dengan
- a & b = panjang sisi yang sejajar
- t = tinggi
- c = panjang sisi miring
Pada trapesium siku-siku, banya terdapat satu buah c, sehingga kelilingnya menyesuaikan.
Pelajari lebih lanjut di Trapesium.
6. Layang-layang
Merupakan sebuah bangun datar dengan 2 pasang sisi yang sama panjang dan memiliki 2 buah diagonal bidang yang tidak sama panjang.
Gambar layang-layang adalah sebagai berikut:
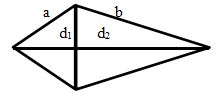
dengan rumus luasnya yaitu:
L = ½ × d1 × d2
dan rumus kelilingnya yaitu:
K = 2(a + b)
dengan
- a & b = panjang sisi miring
- d1 dan d2 = diagonal 1 dan 2.
Pelajari lebih lanjut di Layang-Layang.
7. Belah ketupat
Merupakan sebuah bangun datar dengan 2 pasang sisi yang sama panjang dan memiliki 2 buah diagonal bidang yang tidak sama panjang.
Gambar belah ketupat adalah sebagai berikut:
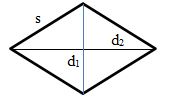
dengan rumus luasnya yaitu:
L = ½ × d1 × d2
dan rumus kelilingnya yaitu:
K = 4 . s
dengan
- s = panjang sisi
- d1 dan d2 = diagonal 1 dan 2.
Pelajari lebih lanjut di Belah Ketupat.
8. Lingkaran
Merupakan sebuah bangun datar yang mana terbentuk dari kumpulan titik yang berjarak sama dengan titik pusatnya.
Gambar lingkaran adalah sebagai berikut:
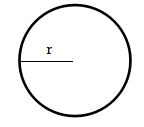
dengan rumus luasnya yaitu:
L = π × r2
dan rumus kelilingnya yaitu:
K = 2πr = πd
dengan
- π (pi) = 3,14 = 22/7
- r = jari-jari
- d = diameter
Contoh Soal Geometri
Hitunglah luas dan keliling bangun di bawah ini.
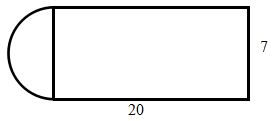
L = Lpersegi panjang + Lsetengah lingkaran
L = 20.7 + 22/7 × 7/2 × 7/2
L = 140 + 38,5
L = 178,5 satuan luas
K = 20 + 7 + 20 + 22/7 × 7
K = 68 satuan panjang
Sekian pembahasan terkait geometri pada dimensi 1 dan 2 pada kesempatan ini, semoga dapat dijadikan bahan tambahan untuk belajar.