Garis dan Sudut: Pengertian, Jenis-jenis, Contoh Soal
Kali ini kita akan belajar mengenai garis dan sudut.
Garis dan sudut merupakan salah satu materi yang menjadi dasar untuk mempelajari materi-materi geometri yang lain.
Dengan memahami konsep garis dan sudut, kalian akan dapat dengan mudah mempelajari konsep bidang, bangun datar, dan materi geometri yang lainnya.
Perhatikan penjelasan mengenai garis berikut.
Garis
Perhatikan gambar berikut.
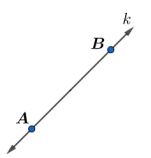
Pada gambar di atas terdapat dua titik yang dihubungkan dengan garis. Terdapat garis yang ujung-ujungnya terdapat anak panah, menandakan bahwa panjang garis adalah tak terbatas.
Garis di atas melalui dua titik, yaitu titik A dan titik B. Pemberian nama garis dapat dilakukan dengan dua cara.
Pertama, kalian dapat memberi nama garis dengan menyebutkan dua titik yand dilalui garis tersebut. Misalnya pada gambar di atas titik A dan titik B merupakan dua titik yang dilalui garis, sehingga kita dapat menuliskannya sebagai garis AB, atau jika disimbolkan menjadi ![]() .
.
Kemudian cara pemberian nama yang kedua yaitu memberi nama garis dengan simbol huruf kecil (bukan huruf kapital).
Pada gambar di atas terdapat huruf k sebagai nama garis, sehingga kita dapat menyebutnya sebagai garis k.
Lalu, apa yang di maksud dengan garis itu?
Untuk mengetahuinya silakan pahami penjelasan di bawah ini.
Pengertian Garis
Apakah kalian mengetahui apa itu garis?
Sebenarnya titik, garis, dan bidang dalam geometri tidak memiliki definisi atau pengertian yang pasti (mutlak).
Akan tetapi untuk memudahkan pemahaman mengenai hal tersebut, terdapat beberapa istilah tidak formal yang digunakan.
Garis dapat didefinisikan sebagai kumpulan/himpunan titik-titik yang berjejer dan terhubung secara kontinu.
Selanjutnya akan dibahas mengenai penerapan garis dalam kehidupan sehari-hari.
Garis dalam Kehidupan Sehari-Hari
Banyak sekali penerapan garis dalam kehidupan sehari-hari. Bentuk-bentuk geometris banyak menerapkan konsep garis dalam pembuatannya.
Selain itu, dalam mempelajari persamaan garis, dapat menerapkan konsep garis untuk membantu dalam visualisasi garis pada koordinat kartesius.
Sketsa atau rancangan gambar yang dibuat banyak menerapkan/menggunakan garis, dan masih banyak penerapan garis yang lainnya.
Selanjutnya akan dibahas mengenai sudut.
Sudut
Perhatikan gambar berikut.
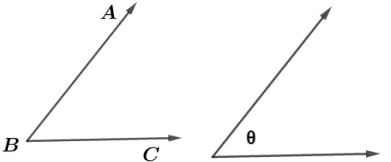
Pada gambar di atas terdapat sudut dan tiga titik yaitu titik A, titik B, dan titik C. Pemberian nama sudut mengacu pada ketiga titik tersebut.
Pemberian nama sudut ada dua cara yaitu dengan menyebutkan tiga titik pada sudut atau hanya menyebutkan huruf yang ada pada titik sudutnya.
Misalnya pada gambar di atas, sudut di atas dapat kita beri nama dengan sudut ABC atau cukup dengan menyebutkan sudut B (∠ABC atau ∠B). Selain itu juga terdapat pemberian nama sudut dengan menggunakan symbol seperti alpha (α), beta (β), gamma (γ), tetha (θ), dan symbol lainnya.
Selanjutnya akan dijelaskan mengenai definisi sudut.
Pengertian Sudut
Perhatikan gambar berikut.
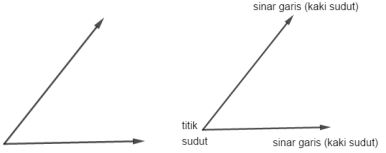
Apa itu sudut?
Sudut adalah suatu objek geometri yang tersusun dari dua sinar garis dengan kedua pangkal sinar garis tersebut bertemu pada satu titik.
Kedua sinar garis tersebut merupakan kaki-kaki sudut dan titik pertemuan kedua pangkal sinar garis merupakan titik sudut.
Selanjutnya akan dijelaskan mengenai jenis-jenis sudut.
Jenis-Jenis Sudut
Pada bagian ini akan dijelaskan mengenai jenis-jenis sudut berdasarkan besar sudutnya.
1. Sudut lancip
Perhatikan gambar berikut.
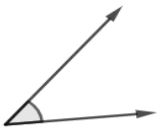
Sudut lancip merupakan jenis sudut dengan ukuran sudut antara 0° – 90° (kurang dari 90°).
2. Sudut siku-siku
Perhatikan gambar berikut.
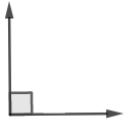
Pada gambar di atas terdapat sudut siku-siku. Sudut siku-siku memiliki besar sudut 90°.
3. Sudut tumpul
Perhatikan gambar berikut.
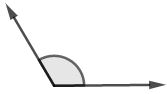
Sudut tumpul merupakan salah satu jenis sudut dengan ukuran sudut lebih dari 90° dan kurang dari 180°.
4. Sudut lurus
Perhatikan gambar berikut.

Gambar di atas merupakan sudut lurus dengan besar sudut 180°.
5. Sudut refleks
Perhatikan gambar berikut.
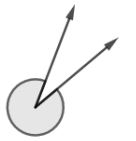
Gambar di atas merupakan gambar sudut refleks. Sudut refleks memiliki besar sudut lebih dari 180° dan kurang dari 360°.
Selanjutnya akan dibahas mengenai hubungan antar garis.
Hubungan Antar Sudut
Perhatikan gambar berikut.
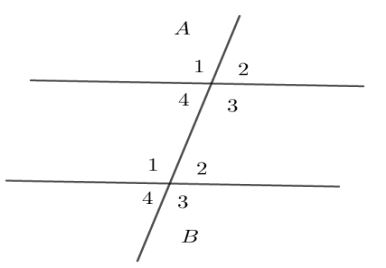
Pada gambar di atas terdapat delapan sudut yang masing-masing diberi nama sudut dengan kode A1, A2, A3, A4, B1, B2, B3, B4, B5.
Beberapa hubungan antar sudut yaitu sebagai berikut.
1. Sudut sehadap
A1 dengan B1, A2 dengan B2, A3 dengan B3, dan A4 dengan B4. Besar dua sudut sehadap adalah sama.
2. Sudut dalam sepihak
A4 dengan B1, A3 dengan B2. Jumlah sudut dalam sepihak adalah 180 derajat.
3. Sudut luar sepihak
A1 dengan A4, A2 dengan B3. Jumlah sudut luar sepihak adalah 180 derajat.
4. Sudut bertolak belakang
A1 dengan A3, A2 dengan A4, B1 dengan B3, dan B2 dengan B4. Besar dua sudut yang bertolak belakang adalah sama.
5. Sudut berpelurus
A1 dengan A2, A3 dengan A4, B1 dengan B2, B3 dengan B4. Jumlah besar sudut yang berpelurus adalah 180 derajat.
6. Sudut dalam berseberangan
A4 dengan B2 dan A3 dengan B1. Besar sudut dalam berseberangan adalah sama.
7. Sudut luar berseberangan
A1 dengan B3 dan A2 dengan B4. Besar sudut luar berseberangan adalah sama.
Coba kerjakan soal berikut untuk meningkatkan pemahaman mengenai garis dan sudut.
Baca juga Transformasi Geometri.
Contoh Soal Garis dan Sudut
Perhatikan gambar berikut.

Soal 1. Tentukan hubungan antar sudut berdasarkan gambar di atas.
- Sudut A1 dengan sudut B3.
- Sudut A3 dengan sudut B1.
- Sudut A2 dengan sudut A4.
- Sudut B4 dengan sudut A4.
- Sudut luar berseberangan
- Sudut dalam berseberangan
- Sudut bertolak belakang
- Sudut sehadap
Soal 2. Jika besar sudut A3 adalah 105°, besar sudut B2 adalah . . .
Besar sudut B2:
Sudut A3 dan sudut B2 merupakan dua sudut dalam sepihak yang jumlahnya 180 derajat, sehingga besar sudut B2 adalah 180° – 105° = 75°
Mari kita simpulkan bersama materi mengenai garis dan sudut.
Kesimpulan
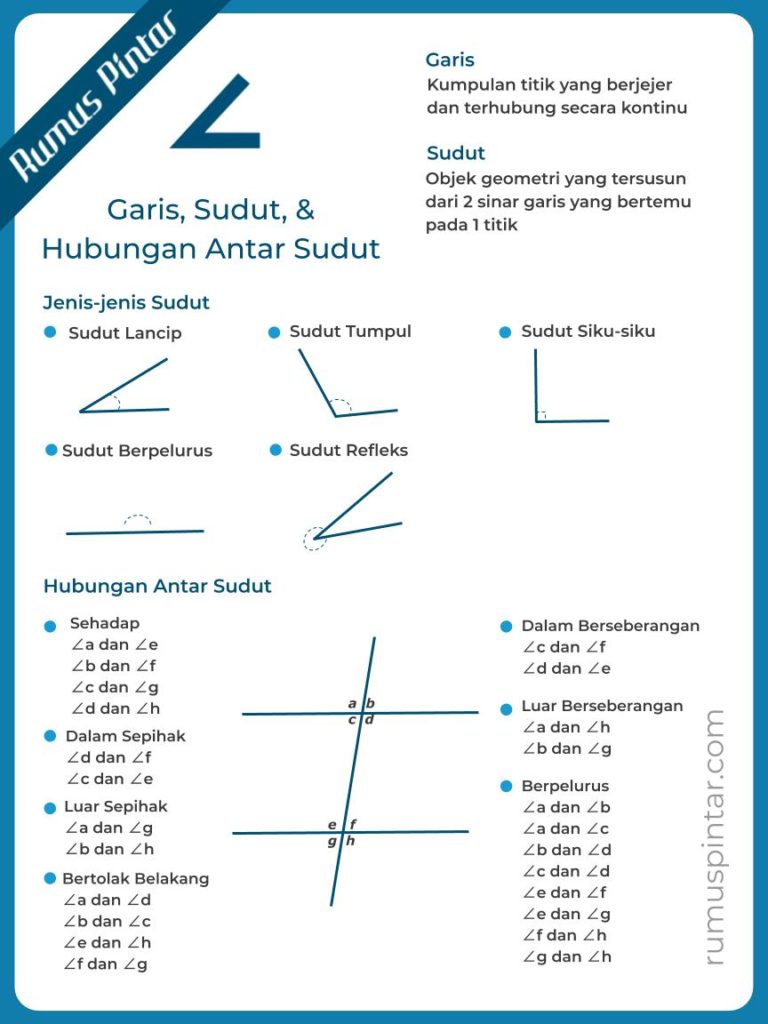
Garis dapat didefinisikan sebagai kumpulan/himpunan titik-titik yang berjejer dan terhubung secara kontinu.
Sudut adalah suatu objek geometri yang tersusun dari dua sinar garis dengan kedua pangkal sinar garis tersebut bertemu pada satu titik. Kedua sinar garis tersebut merupakan kaki-kaki sudut dan titik pertemuan kedua pangkal sinar garis merupakan titik sudut.
Jenis-jenis sudut berdasarkan besar sudutnya yaitu sudut lancip, sudut siku-siku, sudut tumpul, sudut lurus, dan sudut refleks.
Hubungan antar sudut meliputi sudut yang sehadap, bertolak belakang, sepihak, luar sepihak, dalam berseberangan, dan luar berseberangan.
Demikian penjelasan mengenai garis dan sudut, semoga bermanfaat.