Persamaan Kuadrat

 Persamaan Kuadrat: Pengertian, Rumus, & Materi

Materi yang akan kita bahas hari ini yaitu mengenai persamaan kuadrat. Langsung saja, simak materi persamaan kuadrat berikut.

Sebelumnya kalian pasti pernah belajar mengenai perkalian bentuk aljabar dan pemfaktorkan bentuk aljabar.

Apa yang kalian pelajari dalam perkalian bentuk aljabar dan pemfaktoran bentuk aljabar?

Salah satunya kalian mengenal adanya bentuk kuadrat. Untuk menambah pengetahuan kalian, akan dibahas mengenai persamaan kuadrat pada bagian berikut.

Pengertian Persamaan Kuadrat

Apakah kalian mengetahui tentang persamaan kuadrat?

Persamaan kuadrat secara sederhana dapat dipahami sebagai bentuk polinomial dengan pangkat tertinggi 2.

Bentuk umum persamaan kuadrat yaitu ax2 + bx + c = 0 dengan a ≠ 0.

Dari bentuk persamaan umum di atas, jika digambarkan dalam bentuk grafik maka grafik akan berbentuk parabola.

Bentuk grafik persamaan kuadrat tersebut berdasarkan pada nilai koefisien dan konstanta persamaan kuadratnya.

Koefisien a menentukan tingkat kecekungan parabola.

Nilai a > 0 menunjukkan grafik parabola yang terbuka ke atas, sedangkan nilai a < 0 menunjukkan grafik parabola yang terbuka ke bawah.

Koefisien b menetukan posisi titik puncak terhadap absis (sumbu-x) pada grafik dan sumbu simetrinya.

Konstanta c menentukan titik potong grafik dengan sumbu-x dan sumbu-y.

Perhatikan contoh penerapan konsep persamaan kuadrat berikut.

Persamaan Kuadrat dalam Kehidupan Nyata

Beberapa permasalahan yang terjadi dalam kehidupan sehari-hari dapat diselesaikan dengan menerapkan konsep persamaan kuadrat ini.

Salah satu contohnya yaitu permasalahan di bawah ini.

Tiko dan Riko bersama-sama menyelesaikan suatu pekerjaan dalam waktu 18 menit. Jika Tiko bekerja sendiri, maka Tiko membutuhkan waktu 15 menit lebih lama daripada waktu yang dibutuhkan Riko. Berapa masing-masing waktu yang dibutuhkan Tiko dan Riko untuk menyelesaikan pekerjaan tersebut?

Nah, permasalahan tersebut dapat diselesaikan dengan menerapkan konsep persamaan kuadrat ini.

Agar kalian dapat menyelesaikan permasalahan yang berkaitan dengan persamaan kuadrat, coba pahami terlebih dahulu materi persamaan kuadrat berikut.

Persamaan dan Fungsi Kuadrat

Apa perbedaan persamaan kuadrat dan fungsi kuadrat?

Seperti yang telah disampaikan pada bagian sebelumnya, bentuk umum persamaan kuadrat yaitu ax2 + bx + c = 0 dengan a ≠ 0.

Sedangkan bentuk umum dari fungsi kuadrat adalah f(x) = ax2 + bx + c = 0 dengan a ≠ 0.

Fungsi kuadrat lebih menjelaskan pada input-output. Ketika kita menentukan suatu nilai untuk variabel (misal: x), maka fungsi kuadrat menghasilkan output berupa nilai tertentu.

Penjelasan mengenai beberapa rumus persamaan kuadrat akan disampaikan pada bagian di bawah ini.

Rumus Persamaan Kuadrat

Pada bagian berikutnya akan dibahas mengenai akar-akar persamaan kuadrat.

Sebelum membahas mengenai akar-akar persamaan kuadrat, terlebih dahulu akan dijelaskan rumus menentukan titik puncak parabola.

Bentuk umum persamaan kuadrat: ax2 + bx + c = 0 dengan a ≠ 0.

Titik puncak parabola terhadap absis (sumbu-x) dapat ditentukan dengan

xp = – b / 2a

Titik puncak parabola terhadap ordinat (sumbu-y) dapat ditentukan dengan mensubstitusi nilai x dari xp pada persamaan kuadrat yp = f (x) = ax2 + bx + c = 0.

Atau dapat juga ditentukan dengan yp = – D / 4a, dengan D merupakan diskriminan (D = b2 – 4ac).

Sehingga

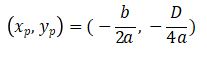
Akar-Akar Persamaan Kuadrat

Sebelum mempelajari akar-akar persamaan kuadrat, akan dijelaskan mengenai sifat-sifat diskriminan berdasarkan nilainya. Bentuk umum persamaan kuadrat: ax2 + bx + c = 0 dengan a ≠ 0. Diskriminan dapat ditentukan dengan D = b2 – 4ac.

• Jika nilai D > 0, maka persamaan kuadrat mempunyai dua akar nyata (real).
• Jika nilai D = 0, maka persamaan kuadrat mempunyai dua akar sama (kembar).
• Jika nilai D < 0, maka persamaan kuadrat tidak mempunyai akar nyata (mempunyai akar imajiner).

Terdapat 3 metode untuk menentukan akar-akar persamaan kuadrat:

• Metode pemfaktoran
• Metode melengkapkan kuadrat sempurna
• Metode rumus ABC

Metode Pemfaktoran

Bentuk umum persamaan kuadrat yaitu ax2 + bx + c = 0 dengan a ≠ 0.

Penentuan akar-akar persamaan kuadrat dengan metode pemfaktoran, hasil akhir pemfaktoran berbentuk a(x – x1)(x – x2) = 0.

Pada bentuk tersebut, x1 dan x2 merupakan akar-akar persamaan kuadrat. Biar lebih jelas, yuk nonton videonya berikut.

Metode Melengkapkan Kuadrat Sempurna

Penyelesaian akar-akar persamaan kuadrat berbentuk ax2 + bx + c dengan melengkapkan kuadrat sempurna dapat dilakukan dengan mengubahnya menjadi bentuk (x + p)2 = q.

Setelah itu, dapat diselesaikan dengan (x + p) = √q dan -(x + p) = √q.

Metode Rumus ABC

Rumus ABC dituliskan sebagai berikut.

Bentuk umum persamaan kuadrat: ax2 + bx + c = 0 dengan a ≠ 0.

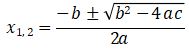
Untuk mengetahui sejauh mana pemahaman kalian mengenai persamaan kudrat, coba kerjakan latihan soal berikut. Baca juga Diagram.

Contoh Soal Persamaan Kuadrat

1. Persamaan kuadrat x2 – 3x + 4 = 0 memiliki titik puncak pada koordinat … .

Pembahasan

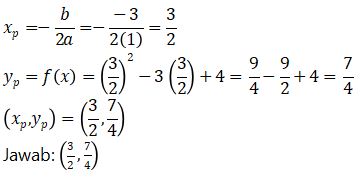
2. Terdapat persamaan kuadrat 2x2 – 2x – 12 = 0. Tentukan akar-akar persamaan kuadrat tersebut menggunakan metode pemfaktoran, metode melengkapkan kuadrat dan menggunakan rumus ABC.

Pembahasan

Metode pemfaktoran

2x2 – 2x – 12 = 0

2(x2 – x – 6) = 0

2x2 – 2x – 12 = 0

2(x – 3)(x + 2) = 0

x – 3 = 0 atau x + 2 = 0

x = 3 atau x = -2

Akar-akar persamaan kuadrat: 3 dan -2

Metode melengkapkan kuadrat sempurna

Menggunakan rumus ABC

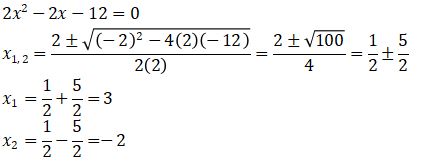
Akar-akar persamaan kuadrat: 3 dan -2.

Read More

Eksponen

 Eksponen: Pengertian, Rumus, & Contoh Soal

4 x 4 x 4 x 4 x 4

Bagaimana kamu membuat bentuk perkalian diatas agar menjadi lebih ringkas?

Yap, bentuk diatas dapat kita tuliskan sebagai 45 yang dibaca 4 pangkat 5. Perpangkatan merupakan kata lain dari eksponen.

Nah, kali ini mari kita simak pembahasan lebih lanjut mengenai eksponen.

Pengertian Eksponen Matematika

Eksponen atau yang lebih sering kita dengar dengan sebutan pangkat adalah nilai yang menunjukkan derajat kepangkatan atau sebanyak berapa kali sebuah bilangan dikalikan dengan bilangan tersebut.

Jika terdapat dua bilangan a dan b, maka notasi dari eksponen matematika adalah ab yang kemudian dibaca a pangkat b.

Jika b merupakan bilangan bulat positif, maka eksponen dapat dinyatakan

ab = a x a x a x … x a  (a sejumlah b faktor)

Sifat sifat eksponen

Eksponen atau pangkat memiliki beberapa sifat, diantaranya :

1. a0= 1 (Eksponen Nol)
2. a-p = 1/ap (Eksponen Negatif)
3. ap/q=q√ap (Eksponen Pecahan)
4. ap x aq = ap+q
5. ap/aq=ap-q
6. (ap)q=apq
7. (am.bn)p = amp. bnp
8. (am/an)p = amp/anp

Fungsi Eksponen dan Grafiknya

Apabila terdapat bilangan real x, maka fungsi eksponen merupakan fungsi yang memetakan bilangan x ke ax dengan syarat a>0 dan a≠1 atau dapat dituliskan f:(x)=ax.

Untuk grafiknya adalah

Grafik Monoton Turun	Grafik Monoton Naik

Fungsi eksponen tersebut memiliki sifat diantaranya

1. Kurva berada diatas sumbu x (definit positif)
2. Memotong sumbu y pada (0,1)
3. Mempunyai asimto y=0 (sb. X)
4. Untuk x>1, maka grafik monoton naik
5. Untuk 0<x<1, maka grafik monoton turun

Persamaan Fungsi Eksponen

Seperti fungsi fungsi lain, dalam materi fungsi eksponen juga terdapat persamaan fungsi eksponen.

Nah, untuk a>0 dan a≠1, beberapa bentuk dari persamaan fungsi eksponen dan penyelesaiannya adalah

1. Jika af(x) = an maka f(x) = n
2. jika ag(x) = ah(x) maka g(x) = h(x)
3. jika af(x)=bf(x) maka f(x) = 0
4. jika f(x)g(x)=f(x)h(x) maka kemungkinan penyelesaiannya adalah
5. g(x) = h(x)
6. f(x) = 1
7. f(x) = -1 jika g(x) dan h(x) sama sama ganjil atau genap
8. f(x) = 0 jika g(x)>0 dan h(x)<0
9. jika f(x)h(x)=g(x)h(x) maka kemungkinan penyelesaiannya adalah
10. f(x) = g(x)
11. h(x) = 0 jika g(x) dan h(x) tidak sama dengan 0
12. jika f(x)g(x)=1 maka kemungkinan penyelesaiannya adalah
13. f(x) = 1
14. g(x) = 0 jika f(x)≠0
15. f(x) = -1 jika g(x) genap

Baca juga Persamaan Linear.

Pertidaksamaan Fungsi Eksponen

Jika ada persamaan fungsi eksponen, maka terdapat pula pertidaksamaan fungsi eksponen. Penyelesaian dari pertidaksamaan fungsi eksponen adalah sebagai berikut

1. untuk a>1
2. jika af(x)<ag(x) maka f(x)<g(x)
3. jika af(x)>ag(x) maka f(x)>g(x)
4. untuk 0<a<1
5. jika af(x)<ag(x) maka f(x)>g(x)
6. jika af(x)>ag(x) maka f(x)<g(x)

Contoh Soal Fungsi Eksponen

1. x3 . x5 = x(3+5) = x8

2. (x3.y2)2 = x3.2 . y2.2 = x6.y4

3. Jika f(x) = 3x+2 cari nilai f(3) dan f(-3)

• f(3) = 33+2 = 35 = 243
• f(-3) = 3-3+2 = 3-1= 1/3 = 0,333

4. Cari nilai x yang memenuhi 3x-3 = 0

• 3x-3 = 0
• 3x =31
• x = 1 maka x yang dicari adalah x=1

5. Tentukan nilai x yang memenuhi persamaan eksponen 4x+2+4x=17 !

Pembahasan

4x+2 + 4x=17

4x.42 + 4x=17

16.4x + 4x = 17

17.4x = 17

4x = 1

x = 0

Jadi, nilai x yang memenuhi persamaan eksponen 4x+2+4x=17 adalah 0

6. Akar-akar persamaan 253x-6 = 54x^2−12x+2 adalah p dan q. Berapakah nilai pq?

Pembahasan

253x-6 = 54x^2−12x+2

52(3x-6) = 54x^2−12x+2

2(3x-6) = 4x2 − 12x + 2

6x – 12 = 4x2 − 12x + 2

4x2 − 12x + 2 – 6x + 12 = 0

4x2 − 18x +14 = 0

pq = c/a = 14/4 = 3,5

Jadi, nilai pq adalah 3,5.

7. Diketahui 32x – 1 – 1 = 2.3x-1. Hitunglah nilai 9x!

Pembahasan

32x – 1 – 1 = 2.3x-1

32x /31 – 1 = 2.3x /31

32x – 3 = 2.3x

32x -2.3x – 3 = 0

Misal a = 3x, maka

32x – 2.3x – 3 = 0

a2 – 2a – 3 = 0

(a-3)(a+1) = 0

a = 3 atau a = -1

Karena, a = -1 tidak mungkin memenuhi a = 3x, maka a = 3.

Sehingga

a = 3x

3 = 3x

31 = 3x

x = 1

9x = 91 = 9

Jadi, nilai dari 9x adalah 9.

8. Jika 3x – y = 81 dan 2x – 2y = 1/16, tentukan nilai x+y!

Pembahasan

3x – y = 81

3x – y = 34

x – y = 4

x = y + 4 … (1)

2x – 2y = 1/16

2x – 2y = 2-4

x – 2y = -4 … (2)

Substitusikan (1) ke (2), sehingga diperoleh

x – 2y = 4

y + 4 – 2y = -4

-y = -8

y = 8

Substitusikan nilai y ke (1), sehingga diperoleh

x = y + 4

x = 8 + 4

x = 12

x + y = 8 + 12 = 20

Jadi, nilai x + y adalah 20.

9. Tentukan nilai 31/n jika diketahui (90,125)n = √3.

Pembahasan

(90,125)n = √3

90,125n = √3

32(0,125)n = 3½

30,25n = 3½

0,25n = ½

n = 2

Sehingga diperoleh

31/n = 3½ = √3

Jadi, nilai 31/n adalah √3.

Read More

Sistem Bilangan

 Sistem Bilangan: Pengertian, Macam-macam, Soal

July 10, 2022 by Wisnu

Pada kesempatan ini, kita akan membahas secara singkat mengenai sistem bilangan. Mungkin istilah ini tidak asing di telinga teman-teman sekalian karena memang sistem bilangan merupakan cara untuk menuliskan suatu bilangan.

Selain itu, dapat kita katakan bahwa sistem bilangan merupakan simbol yang digunakan untuk menerangkan hal secara detail melalui angka.

Dalam pembahasan kali ini, akan disampaikan sedikit mengenai 4 (empat) macam sistem bilangan, yaitu sistem bilangan biner, sistem bilangan desimal, sistem bilangan oktal, dan sistem bilangan heksadesimal.

Sistem Bilangan Biner

Bagi teman-teman yang senang dengan komputasi, pasti tidak asing dengan yang dinamakan sistem bilangan biner.

Bilangan biner sendiri adalah angka yang terdiri dari dua angka yaitu 0 dan 1, atau biasa disebut dengan bilangan berbasis 2.

Sehingga, dapat dikatakan bahwa sistem bilangan biner adalah sistem bilangan dengan hanya menggunakan bilangan biner.

Sistem bilangan biner ini biasanya digunakan untuk mempersentasikan alat-alat yang memiliki dua keadaan operasi yang berlawanan.

Misalnya lampu pijar pada keadaan terang atau gelap, laptop dalam keadaan menyala atau mati, dan kipas angin dalam keadaan berputar atau diam.

Penulisan bilangan biner adalah sebagai berikut:

0, 1, 10, 11, 100, 101, 110, 111, …

Sistem bilangan desimal

Bilangan desimal adalah bilangan yang pastinya sudah pernah teman-teman kenal sebelumnya, yang mana bilangan desimal adalah bilangan yang menggunakan sepuluh simbol angka, yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9, atau biasa disebut dengan bilangan berbasis 10.

Sehingga, dapat dikatakan bahwa sistem bilangan desimal adalah sistem bilangan yang menggunakan bilangan desimal.

Pada sistem bilangan ini, posisi dari suatu bilangan akan menentukan nilainya. Penulisannya adalah sebagai berikut:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …

Kemudian, penentuan nilai menggunakan posisi adalah sebagai berikut:

100, 101, 102, 103, …, 10n

Dapat kita pahami bahwa 100 > 101 > 102 > 103 > … > 10n.

Sistem Bilangan Oktal

Sistem bilangan oktal adalah sistem bilangan yang menggunakan bilangan oktal, yang mana bilangan oktal tersebut terdiri dari delapan simbol angka yaitu 0, 1, 2, 3, 4, 5, 6, dan 7, atau biasa disebut dengan bilangan berbasis 8.

Bilangan oktal juga dapat digunakan untuk menyederhanakan bilangan biner, seperti 8 = 23 yang berarti satu digit bilangan oktal dapat mewakili tiga digit bilangan biner.

Penulisan bilangan oktal adalah sebagai berikut:

1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, …

Sistem Bilangan Heksadesimal

Sistem bilangan yang menggunakan bilangan heksa desimal yang mana berbasis 16 dengan angka-angkanya yaitu 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, dan F.

Sistem bilangan ini identic dengan sistem bilangan oktal, sehingga sistem bilangan heksadesimal dapat digunakan untuk menjadi alternative dalam menyederhanakan bilangan biner.

Misalnya 16 = 24, artinya satu digit bilangan heksadesimal dapat mewakili empat digit bilangan biner.

Contoh soal Sistem Bilangan

Konversikan bilangan oktal 64 menjadi bentuk biner.

Pembahasan

64 = 2n

26 = 2n

n = 6

Read More

Bola

Bola: Rumus Luas Permukaan, Rumus Volume, Contoh

Artikel kali ini akan membahas mengenai bangun ruang bola. Pada materi bangun datar, kalian telah mempelajari mengenai bangun lingkaran.

Apa saja unsur-unsur yang terdapat dalam lingkaran?

Apakah kalian masih mengingatnya?

Salah satu unsur dalam lingkaran adalah jari-jari. Nah, pada kesempatan kali ini kita akan membahas mengenai salah satu bangun ruang yang juga memiliki unsur jari-jari.

Bangun ruang apakah itu? Simak penjelasan di bawah ini.

Definisi Bola

Perhatikan gambar berikut.

Salah satu bangun ruang yang unsurnya merupakan jari-jari yaitu bangun ruang bola.

Apa itu bangun ruang bola?

Bola merupakan salah satu bangun ruang sisi lengkung yang tersusun dari tak terhingga banyaknya lingkaran yang berpusat di satu titik yaitu titik pusat bola.

Bola juga dapat diartikan sebagai himpunan semua titik dalam dimensi tiga yang berjarak sama dengan suatu titik acuan, yaitu titik pusat bola.

Selanjutnya, perhatikan beberapa contoh penerapan bola dalam kehidupan sehari-hari.

Bola dalam Kehidupan Sehari-hari

Terdapat banyak contoh penerapan bola dalam kehidupan sehari-hari.

Beberapa objek yang berbentuk menyerupai bola seperti bola basket, bola kasti, kelereng, dan objek yang menyerupai lingkaran lainnya.

Selanjutnya akan dijelaskan mengenai sifat-sifat bola.

Sifat-Sifat Bola

Perhatikan gambar bangun bola di bawah ini.

Pada gambar tersebut terdapat beberapa ciri-ciri atau karakteristik yang membedakan antara bangun ruang bola dengan bangun-bangun ruang lainnya.

Apa sajakah karakteristik tersebut?

Berikut merupakan karakteristik bangun ruang bola.

• Bangun ruang bola memiliki satu sisi. Sisi bola merupakan kumpulan titik-titik yang berjarak sama dengan pusat bola. Sisi bola tersebut dapat disebut sebagai permukaan bola atau selimut bola.
• Bangun ruang bola tidak memiliki rusuk.
• Pada gambar di atas, bagian yang diberi nama dengan r merupakan jari-jari bola. Jari-jari bola menghubungkan titik pusat bola dengan titik pada permukaan bola.
• Sama dengan materi pada bangun lingkaran, diameter bola ukurannya dua kali ukuran jari-jari bola.
• Ruang garis yang menghubungkan dua titik pada bola disebut dengan tali busur bola. Tali busur bola terpanjang merupakan diameter bola.

Rumus Bola

Berikut akan dijelaskan beberapa rumus yang digunakan dalam materi bangun ruang bola. Rumus yang akan kita bahas pada bagian ini adalah rumus luas permukaan bola dan rumus volume bola.

Perhatikan gambar berikut.

Pada gambar di atas, jari-jari bola ditunjukkan oleh ruas garis OA dan titik pusat bola ditunjukkan oleh titik O. Titik A terletak pada permukaan bola.

Rumus Volume Bola

Volume bola dirumuskan sebagai:

Rumus Volume Bola

V = (4/3) x π x r3

Keterangan:

V : Volume bola

r  : jari-jari bola

π : konstanta yang bernilai 3,14159 . . .

Coba kerjakan soal berikut untuk meningkatkan pemahaman kalian mengenai bangun ruang bola.

Contoh Soal Bola

1. Terdapat suatu bola dengan jari-jari 21 cm. Tentukan luas permukaan dan volume bola tersebur. (Gunakan π = 22/7).

Pembahasan

Diketahui: r = 21 cm.

Lp = 4 x π x r2 = 4 x (22/7) x 21 cm x 21 cm = 5.544 cm2

V = (4/3) x π x r3 = (4/3) x (22/7) x 21 cm x 21 cm x 21 cm = 38.808 cm3.

2. Terdapat dua buah bola dengan jari-jari bola masing-masing adalah 4 cm dan 12 cm. Tentukan perbandingan volume dua bola tersebut.

Pembahasan

V = (4/3) x π x r3

Diketahui: r = 4 cm  dan R = 12 cm.

Vkecil/Vbesar = ((4/3) x π x r3)/( (4/3) x π x R3) = r3/R3 = (4 x 4 x 4)/(12 x 12 x 12) = 1/27.

Perbandingan volume dua bola tersebut adalah 1 : 27.

Mari kita simpulkan bersama.

Kesimpulan

• Bola merupakan salah satu bangun ruang sisi lengkung yang tersusun dari tak terhingga banyaknya lingkaran yang berpusat di satu titik yaitu titik pusat bola. Bola juga dapat diartikan sebagai himpunan semua titik dalam dimensi tiga yang berjarak sama dengan suatu titik acuan, yaitu titik pusat bola.
• Rumus luas permukaan bola yaitu Lp = 4 x π x r2.
• Rumus volume bola yaitu V = (4/3) x π x r3.

Demikian pembahasan mengenai bangun ruang bola. Semoga dapat memberikan banyak manfaat bagi pembaca semuanya.

Read More