Lingkaran

Lingkaran: Pengertian, Rumus, Contoh Soal

Masih ingatkah dengan materi bangun datar? Nah, pada artikel ini akan dibahas mengenai salah satu bangun datar yaitu Lingkaran.

Terdapat beberapa bangun datar yang sudah kita kenal, seperti persegi, persegi panjang, segitiga, trapesium, jajar genjang, layang-layang, dan bangun datar yang lainnya.

Salah satu bangun datar yang memiliki sisi lengkung yaitu lingkaran. Berikut penjelasan mengenai lingkaran.

Pengertian Lingkaran

Apa itu lingkaran?

Lingkaran merupakan himpunan titik-titik yang berjarak sama terhadap suatu titik tertentu. Titik tertentu pada lingkaran tersebut disebut sebagai pusat lingkaran.

Lingkaran memiliki satu sisi yang berupa sisi lengkung. Jarak suatu titik pada lingkaran dengan pusat lingkaran disebut sebagai jari-jari lingkaran. Perhatikan gambar berikut.

Pada gambar di atas, titik P merupakan titik pusat lingkaran dan r merupakan jari-jari lingkaran.

Dalam lingkaran juga terdapat ruas garis yang menghubungkan dua titik pada lingkaran disebut sebagai tali busur.

ali busur terpanjang lingkaran melalui titik pusat lingkaran disebut sebagai diameter lingkaran. Panjang diameter lingkaran adalah dua kali Panjang jari-jari lingkaran.

Berikut merupakan contoh penerapan lingkaran.

Penerapan Lingkaran

Konsep mengenai lingkaran banyak diterapkan dalam berbagai bidang. Konsep mengenai luas lingkaran dapat digunakan untuk mengukur luas lahan ataupun luas suatu objek yang berbentuk lingkaran.

Konsep mengenai keliling dapat diterapkan pada pemecahan masalah mengenai jari-jari/diameter roda dengan Panjang lintasan atau jarak yang ditempuh, dan penerapan-penerapan lainnya.

Berikut akan dijelaskan mengenai keliling lingkaran.

Baca juga Bangun Datar.

Keliling Lingkaran

Perhatikan gambar berikut.

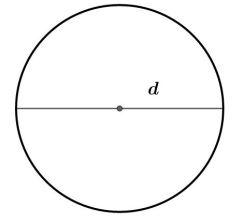
Keliling lingkaran dapat dirumuskan sebagai berikut.

Keliling Lingkaran = π x diameter lingkaran

K = π x d

Karena ukuran diameter adalah dua kali ukuran jari-jari lingkaran, maka diperoleh:

K = π x (2 x r) = 2 x π x r

Keterangan:

• K : keliling lingkaran
• π : phi, konstanta dengan nilai 3,1459…  (22/7)
• d : diameter lingkaran
• r  : jari-jari lingkaran

Berikut akan dijelaskan mengenai luas lingkaran.

Luas Lingkaran

Perhatikan gambar berikut.

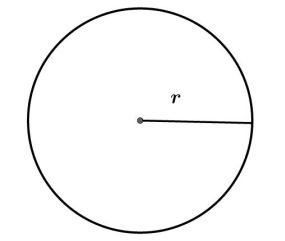
Pada gambar dia atas terdapat lingkaran dengan jari-jari r. Luas lingkaran dirumuskan sebagai berikut.

Luas lingkaran = π x jari-jari lingkaran x jari-jari lingkaran

L = π x r x r

L = π x r2

Hubungannya dengan diameter dirumuskan sebagai

L = π x (1/2 d)2

L = ¼ x π x d2

Keterangan:

• K : keliling lingkaran
• π : phi, konstanta dengan nilai 3,1459…  (22/7)
• d : diameter lingkaran
• r  : jari-jari lingkaran

Berikut ini akan dijelaskan mengenai persamaan lingkaran.

Baca juga Segi Empat.

Persamaan Lingkaran

Pada bagian ini akan dijelaskan mengenai persamaan lingkaran berjari-jari r dengan pusat pada O (0, 0) dan pusat P (a, b).

Persamaan lingkaran yang berpusat di O (0, 0).

Perhatikan gambar berikut.

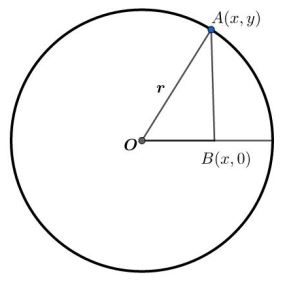
Berdasarkan gambar di atas, persamaan lingkaran dengan pusat O (0, 0) dan jari-jari r yaitu:

Panjang OA = r

Panjang OB = x

Panjang AB = y

Dengan menerapkan konsep phytagoras diperoleh:

OB2 + AB2 = OA2

x2 + y2 = r2

Persamaan lingkaran dengan pusat P (a, b).

Perhatikan gambar berikut.

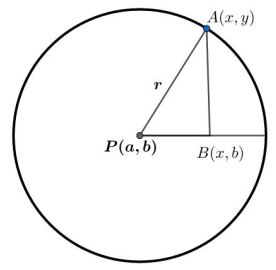
Ukuran  AP = r

Ukuran PB = x – a

Ukuran AB = y – b

Dengan menerapkan konsep Pythagoras diperoleh:

PB2 + AB2 = AP2

(x – a)2 + (y – b)2 = r2

Keterangan:

• (a, b) : koordinat titik pusat lingkaran. a : absis, b : ordinat.
• r : jari-jari lingkaran

Berikut ini akan dijelaskan mengenai persamaan garis singgung lingkaran.

Baca juga Teorema Phytagoras.

Persamaan Garis Singgung Lingkaran

Pembahasan mengenai garis singgung lingkaran akan dibagi menjadi garis singgung dalam dan garis singgung luar lingkaran.

Persamaan garis singgung dalam lingkaran.

Perhatikan gambar berikut.

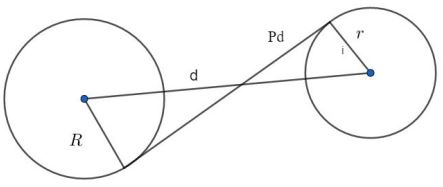
Garis singgung lingkaran dalam dirumuskan sebagai berikut.

Pd = √(d2 – (R + r)2)

Keterangan:

• Pd : garis singgung lingkaran dalam
• d : jarak kedua pusat lingkaran
• R : jari-jari lingkaran besar.
• r : jari-jari lingkaran kecil.

Selanjutnya yaitu Persamaan garis singgung lingkaran luar.

Persamaan Garis Singgung Lingkaran Luar

Perhatikan gambar berikut.

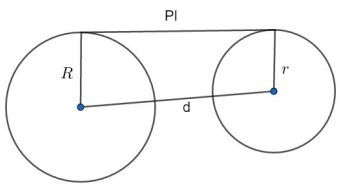
Garis singgung lingkaran luar dirumuskan sebagai berikut.

Pl = √(d2 – (R – r)2)

Keterangan:

• Pl : garis singgung lingkaran luar
• d : jarak kedua pusat lingkaran
• R : jari-jari lingkaran besar.
• r : jari-jari lingkaran kecil.

Untuk meningkatkan pemahaman mengenai lingkaran, perhatikan contoh soal di bawah ini.

Baca juga Geometri.

Contoh Soal Lingkaran

1. Terdapat lingkaran dengan jari-jari 14 cm. Tentukan keliling dan luas lingkaran tersebut.

Pembahasan

r = 14 cm.

K = 2 x π x r = 2 x 22/7 x 14 cm = 88 cm.

L = π x r x r = 22/7 x 14 cm x 14 cm = 616 cm2.

2. Terdapat lingkaran dengan pusat (2, 3) dan berjari-jari 5 cm. Tentukan persamaan lingkaran tersebut.

Pembahasan

Persamaan lingkaran (a, b) = (2, 3) dan r = 5.

(x – 2)2 + (y – 3)2 = 52

x2 + y2 – 4x – 6y – 12 = 0.

3. Dua lingkaran dengan jarak kedua titik pusat 15 cm. Jika jari-jari kedua lingkaran adalah 5 cm dan 4 cm, tentukan Panjang garis singgung persekutuan dalam lingkaran tersebut.

Pembahasan

Pd = √(d2 – (R + r)2)

Pd = √(152 – (5 + 4)2) = √(225 – 81) = √144 = 12 cm

Apa yang sudah kita pelajari mengenai lingkaran?

Kesimpulan

Lingkaran merupakan himpunan titik-titik yang berjarak sama terhadap suatu titik tertentu. Titik tertentu pada lingkaran tersebut disebut sebagai pusat lingkaran.

• Rumus keliling lingkaran yaitu K = π x d.
• Rumus luas lingkaran yaitu L = π x r x r.
• Persamaan lingkaran dengan pusat O (0, 0) dan berjari-jari r yaitu x2 + y2 = r2.
• Persamaan lingkaran dengan pusat P (a, b) dan berjari-jari r yaitu (x – a)2 + (y – b)2 = r2
• Garis singgung persekutuan dalam lingkaran dirumuskan dengan Pd = √(d2 – (R + r)2)
• Garis singgung persekutuan luar lingkaran dirumuskan dengan Pl = √(d2 – (R – r)2)

Demikian pembahasan mengenai lingkaran. Semoga pembahasan dalam artikel ini dapat menambah wawasan kalian mengenai lingkaran. Terima kasih.

Read More

Segitiga

 Segitiga: Pengertian, Rumus Keliling & Luas, Soal

Artikel kali ini akan membahas salah satu bangun datar. Bangun datar apakah itu? Simak penjelasannya.

Banyak sekali macam bangun datar, salah satunya yaitu segitiga. Apakah kalian mengetahui bagaimana bentuk segitiga itu?

Nah, pada artikel ini akan dibahas mengenai segitiga meliputi macam-macam segitiga, rumus yang terkait dengan bangun segitiga, dan pembahasan lainnya.

Berikut akan dijelaskan mengenai pengertian segitiga.

Pengertian Segitiga

Segitiga merupakan salah satu bangun datar yang dibatasi oleh tiga sisi. Perhatikan bangun segitiga berikut.

Pada gambar di atas, terdapat segitiga ABC dengan tiga sisi yaitu sisi AB, BC, dan AC. Memiliki 3 sudut yaitu sudut ABC, sudut BAC, dan sudut ACB, serta memiliki tiga titik sudut yaitu titik A, B, dan C.

Berikut beberapa contoh penerapan segitiga.

Penerapan Segitiga

Apa saja contoh penerapan segitiga yang kalian ketahui?

Konsep segitiga banyak digunakan untuk mempelajari materi-materi matematika yang lain seperti teorem Pythagoras, garis singgung lingkaran.

Beberapa permasalahan terkait luas dan keliling segitiga dapat diselesaikan dengan konsep pada materi ini.

Beberapa luas poligon (segibanyak) juga diselesaikan dengan konsep luas segitiga.

Berikut ini merupakan penjelasan mengenai macam-macam segitiga.

Baca juga Sistem Bilangan.

Macam-Macam Segitiga Berdasarkan Ukuran & Jenisnya

Berdasarkan ukuran dan jenis sisinya, segitiga dibagi menjadi tiga yaitu segitiga sama kaki, segitiga sama sisi, dan segitiga sembarang.

Segitiga Sama Kaki

Segitiga sama kaki merupakan jenis segitiga yang memiliki sepasang sisi yang sama Panjang. Terdapat dua sudut yang sama besar.

Perhatikan gambar segitiga sama kaki di bawah ini.

Pada gambar di atas sepasang sisi yang sama Panjang yaitu sisi AB dan sisi AC. Sedangkan pasangan sudut yang sama besar yaitu sudut ABC dan sudut ACB.

Berikutnya adalah segitiga sama sisi.

Segitiga Sama Sisi

Segitiga sama sisi merupakan segitiga yang ketiga sisi dan sudutnya memiliki ukuran yang sama. Perhatikan gambar berikut.

Pada gambar di atas, ketiga sisi yang sama yaitu sisi AB, sisi BC, dan sisi AC. Ketiga sudutnya juga sama besar yaitu sudut ABC, sudut ACB, dan sudut BAC.

Selanjutnya akan dijelaskan mengenai segitiga sembarang.

Segitiga Sembarang

Segitiga sembarang merupakan jenis segitiga dengan ukuran ketiga sisinya berbeda dan ketiga sudutnya memiliki ukuran yang berbeda pula. Perhatikan gambar berikut.

Pada gambar di atas, sisi AB, sisi BC, dan sisi AC memiliki ukuran sisi yang tidak sama Panjang. Ukuran ketiga sudutnya yaitu sudut ABC, sudut ACB, dan sudut BAC berbeda.

Selanjutnya akan dijelaskan macam-macam segitiga berdasarkan jenis sudutnya.

Baca juga Irisan Kerucut.

Macam-Macam Segitiga Berdasarkan Sudutnya

Berdasarkan ukuran sudutnya, segitiga dibedakan menjadi tiga, yaitu:

Segitiga Lancip

Perhatikan gambar berikut.

Pada gambar di atas terdapat bangun segitiga yang ketiga sudutnya memiliki ukuran kurang dari 90 derajat.

Segitiga Siku-Siku

Perhatikan gambar berikut.

Segitiga siku-siku merupakan jenis segitiga yang salah satu sudutnya memiliki ukuran 90 derajat.  Pada gambar di atas, sudut siku-siku pada segitiga tersebut adalah sudut ABC.

Segitiga Tumpul

Perhatikan gambar segitiga berikut.

Pada segitiga tumpul, terdapat salah satu sudutnya yang berukuran lebih dari 90 derajat. Pada gambar di atas sudut tumpul segitiganya yaitu sudut ABC.

Berikut ini akan dijelaskan rumus segitiga.

Baca juga Lingkaran.

Rumus Segitiga

Rumus segitiga yang akan dibahas meliputi rumus keliling segitiga dan rumus luas segitiga.

Rumus Keliling Segitiga

Perhatikan gambar berikut.

Pada gambar di atas, terdapat segitiga dengan ukuran sisi a, b, dan c. Keliling segitiga dirumuskan sebagai berikut.

K = BC + AC + AB

K = a + b + c

Keterangan:

a, b, c : ukuran sisi-sisi segitiga.

Berikutnya akan dijelaskan mengenai rumus luas segitiga.

Rumus Luas Segitiga

Perhatikan gambar berikut.

Luas segitiga dirumuskan sebagai berikut.

L = ½ x a x t

Keterangan:

• a : ukuran alas segitiga
• t : ukuran tinggi segitiga

Berikut merupakan pembahasan mengenai segitiga istimewa.

Segitiga Istimewa

Segitiga istimewa merupakan segitiga yang memiliki sifat-sifat khusus. Beberapa segitiga dengan sifat khusus seperti segitiga siku-siku, segitiga segitiga sama kaki, serta segitiga sama sisi.

Berikut ini akan dijelaskan mengenai titik berat segitiga.

Titik Berat Segitiga

Titik berat segitiga dapat diartikan sebagai titik pertemuan atau titik potong dari ketiga garis berat segitiga yang ditarik dari titik sudut segitiga. Perhatikan gambar berikut.

Pada gambar di atas terdapat tiga garis berat yaitu garis AD, BE, dan CF yang masing-masing membagi sisi BC, AC, dan AB menjadi dua sama Panjang.

Titik potong ketiga garis berat tersebut merupakan titik berat segitiga yaitu titik O.

Berikut akan dijelaskan mengenai kesebangunan segitiga.

Baca juga Angka Romawi.

Kesebangunan Segitiga

Kesebangunan segitiga merupakan dua buah segitiga dengan perbandingan sisi-sisi yang bersesuaian adalah sama.

Setiap sisi-sisi segitiga yang satu diperbesar/diperkecil dengan perbandingan yang sama. Berikut merupakan beberapa contoh soal segitiga.

Contoh Soal Segitiga

1. Tentukan jenis segitiga berikut berdasarkan ukuran sisi-sisinya.

• a) 4 cm, 5 cm, dan 6 cm.
• b) 7 cm, 6 cm, dan 6 cm.
• c) 9 cm, 9 cm, dan 9 cm.

Pembahasan

a) Segitiga sembarang (Karena tidak ada ukuran sisi yang sama)

b) Segitiga sama kaki (Karena ada 2 ukuran sisi yang sama)

c) Segitiga sama sisi (Karena semua sisi berukuran sama)

2. Suatu segitiga sama kaki memiliki ukuran kaki segitiga 6 cm dan sisi lainnya 5 cm. Tentukan keliling segitiga tersebut.

Pembahasan

K = a + b + c = 6 cm + 6 cm + 5 cm = 17 cm

3. Suatu segitiga memiliki ukuran alas dan tinggi masing-masing 8 cm dan 11 cm. Tentukan luas segitiga tersebut.

Pembahasan

L = ½ x alas x tinggi

L = ½ x 8 cm x 11 cm

L = 44 cm2.

Mari kita simpulkan materi mengenai segitiga.

Kesimpulan

Segitiga merupakan bangun datar yang dibatasi oleh tiga sisi. Terdapat  juga tiga sudut dalam segitiga.

Jenis segitiga menurut ukuran sisinya dibedakan menjadi segitiga sama kaki, segitiga sama sisi, dan segitiga sembarang.

Jenis segitiga menurut ukuran sudutnya dibedakan menjadi segitiga lancip, segitiga siku-siku, dan segitiga tumpul.

Rumus keliling segitiga yaitu K = a + b + c, dengan a, b, c merupakan ukuran sisi-sisi segitiga.

Rumus luas segitiga yaitu L = ½ x a x t, dengan a dan t masing-masing merupakan ukuran alas dan tinggi segitiga.

Read More

Persegi Panjang

 Persegi Panjang: Rumus Luas, Keliling, dan Contoh Soal

Apakah kalian masih ingat dengan materi segibanyak?

Dapatkah kalian menyebutkan contoh segibanyak?

Beberapa contoh segibanyak diantaranya segitiga, segiempat, segilima, dan segibanyak yang lainnya.

Pada pembahasan kali ini akan dijelaskan mengenai salah satu bangun segiempat adalah persegi panjang. Berikut penjelasannya.

Definisi Persegi Panjang

Persegi panjang merupakan salah satu bangun datar segiempat yang memiliki dua pasang sisi sejajar serta keempat sudutnya merupakan sudut siku-siku. Perhatikan gambar berikut.

Gambar 1. Persegi Panjang

Gambar di atas merupakan bangun persegi panjang. Penamaan bangun persegi panjang dengan menggunakan keempat titik sudutnya.

Sebagai contoh, pada gambar persegi panjang di atas dapat kita beri nama dengan persegi panjang ABCD.

Baca juga Persegi

Selanjutnya akan dibahas mengenai penerapan konsep persegi panjang dalam kehidupan sehari-hari.

Persegi Panjang dalam Kehidupan Sehari-hari

Konsep persegi panjang hamper sering kita jumpai dalam kehidupan sehari-hari.

Misalnya saat kita ingin membuat pagar yang mengelilingi halaman rumah yang berbentuk persegi panjang, kita dapat menerapkan konsep keliling persegi panjang.

Selain itu kita dapat menentukan luas tanah maupun luas selembar kertas berbentuk persegi panjang dengan menggunakan konsep luas persegi panjang.

Pembahasan selanjutnya yaitu mengenai sifat-sifat persegi panjang.

Baca juga Materi Matematika

Sifat-Sifat Persegi Panjang

Apakah kalian mengetahui sifat-sifat persegi panjang?

Pada bagian ini akan dijelaskan mengenai sifat-sifat persegi panjang. Perhatikan gambar berikut.

Gambar 2. Sifat-Sifat Persegi Panjang

Berdasarkan gambar di atas, sifat-sifat persegi panjang yaitu sebagai berikut.

• Memiliki empat buah sisi. Dalam persegi panjang ABCD tersebut terdapat empat sisi yaitu sisi AB, BC, CD, dan DA.
• Sisi-sisi yang sejajar dan berhadapan sama panjang. Dalam persegi panjang ABCD, sisi-sisi yang sejajar dan berhadapan adalah sisi AB dengan sisi CD  dan sisi BC dengan sisi AD.
• Memiliki dua diagonal yang sama panjang. Dalam persegi panjang di atas terdapat diagonal AC dan diagonal BD. Kedua diagonal memiliki ukuran yang sama.
• Memiliki empat sudut siku-siku. Dalam persegi panjang ABCD, terdapat sudut ABC, sudut BCD, sudut CDA, dan sudut DAB yang masing-masing berukuran 90o atau sudut siku-siku.
• Memiliki dua simetri lipat dan simetri putar.

Berikutnya merupakan pembahasan mengenai rumus persegi panjang.

Rumus Persegi Panjang

Pada pembahasan rumus persegi panjang di bawah ini akan dijelaskan dua rumus persegi panjang yaitu rumus keliling persegi panjang dan rumus luas persegi panjang.

Perhatikan bangun persegi panjang berikut untuk menentukan rumus keliling dan luas persegi panjang.

Gambar 3. Keliling dan Luas Persegi Panjang

Rumus Keliling Persegi Panjang

Pada gambar persegi panjang di atas terdapat empat sisi dengan ukuran panjang p  dan lebar l. Keliling persegi panjang dapat dihitung dengan menjumlahkan panjang sisi-sisinya.

Rumus Keliling Persegi Panjang

Keliling persegi panjang ABCD = sisi AB + sisi BC + sisi CD + sisi DA

Keliling persegi panjang ABCD = p + l + p + l

K = (p + p) + (l + l)

K = 2p + 2l

K = 2 (p + l)

Keterangan:

• K : Keliling persegi panjang
• p : ukuran panjang persegi panjang
• l  : ukuran lebar persegi panjang

Selanjutnya akan dibahas mengenai rumus luas persegi panjang.

Rumus Luas Persegi Panjang

Luas persegi panjang merupakan area atau daerah di dalam persegi panjang yang dibatasi oleh sisi-sisi persegi panjang.

Perhatikan gambar berikut untuk lebih memahami konsep luas persegi panjang.

Gambar 4.  Luas Persegi Panjang

Pada gambar di atas terdapat persegi panjang yang di dalamnya terdapat persegi-persegi satuan.

Dapatkah kamu menghitung berapa banyak persegi satuan yang berada dalam persegi panjang tersebut?

Dalam persegi panjang tersebut memiliki panjang 5 satuan dan lebar 5 satuan, sehingga dalam persegi panjang ABCD terdapat 15 persegi satuan.

Banyaknya persegi satuan tersebut mewakili luas daerah persegi panjang dengan unit terkecil satuan persegi.

Lalu bagaimana rumus untuk menentukan luas persegi panjang?

Rumus luas persegi panjang dapat dituliskan sebagai berikut.

Rumus Luas Persegi Panjang

Luas persegi panjang ABCD = ukuran sisi panjang x ukuran sisi lebar

Luas persegi panjang ABCD =  AB x BC

L = p x l

Keterangan:

• L  : luas persegi panjang
• p  : ukuran panjang persegi panjang
• l  : ukuran lebar persegi panjang

Coba kerjakan contoh soal di bawah ini untuk mengetahui pemahaman kalian mengenai persegi panjang.

Contoh Soal Persegi Panjang

1. Terdapat suatu persegi panjang dengan panjang 18 cm dan lebar 14 cm. Berapakah keliling persegi panjang tersebut?

Pembahasan

K = 2 x ( p + l)

K = 2 x (18 cm + 14 cm)

K = 2 x 32 cm

K = 64 cm

Jawaban: 64 cm

2. Suatu lapangan sepakbola memiliki ukuran panjang lapangan 50 m dan lebar lapangan 30 m. Tentukan luas lapangan sepakbola tersebut.

Pembahasan

L = p x l

L = 50 m x 30 m

L = 1500 m2

Jawaban: 1500 m2

3. Suatu ruangan berukuran 8 m x 6 m akan dipasangi keramik. Jika ukuran keramik yang akan dipasang adalah 40 cm x 40 cm, berapa banyak keramik yang dibutuhkan?

Pembahasan

Luas ruangan = p x l = 8 m x 6 m = 800 cm x 600 cm = 480000 cm2

Luas satu buah keramik = 40 cm x 40 cm = 1600 cm2

Banyak keramik = 480000 cm2/1600 cm2 = 300 buah keramik.

Mari kita simpulkan bersama-sama.

Kesimpulan

• Persegi panjang merupakan suatu segiempat yang memiliki dua pasang sisi sejajar sama panjang dan keempat sudutnya siku-siku.
• Rumus keliling persegi panjang yaitu

K = 2 x (p + l)

• Rumus luas persegi panjang yaitu

L = p x l

Demikian pembahasan mengenai persegi panjang. Semoga dapat memberikan tambahan pengetahuan dasar untuk mempelajari materi matematika yang lebih kompleks. Terima kasih.

Read More

Persegi

Persegi: Sifat, Rumus Keliling & Luas, Contoh Soal

Pernahkah anda mengamati ubin di rumah anda? Ubin yang menyusun lantai rumah biasanya berbentuk persegi. Kemudian, apa itu persegi? Selengkapnya akan dibahas pada materi berikut ini

Definisi Persegi

Persegi merupakan bentuk bangun datar yang memiliki 4 sisi sama panjang dan semua sudut sudutnya sama besar dan siku-siku.

Kemudian dari pengertian tersebut dapat diperoleh bahwa setiap sudut persegi dibagi dua sama besar oleh diagonalnya, dan setiap diagonalnya tersebut saling tegak lurus.

Lebih jelasnya terdapat pada gambar dibawah ini.

Persegi Dalam Kehidupan Sehari-hari

Di bagian awal sudah disebutkan bahwa ubin merupakan salah satu contoh penerapan persegi dalam kehidupan sehari hari.

Contoh lain yang dapat kita amati adalah kertas origami, sisi pada dadu, sisi pada rubik, dll.

Baca juga Segi Enam.

Sifat Sifat Persegi

Persegi memiliki sifat sebagai berikut

1. Memiliki 4 sisi sama panjang
2. Setiap sudut yang terbentuk oleh sisinya merupakan sudut siku-siku
3. Setiap diagonalnya membagi 2 sama besar sudut yang terbentuk oleh sisinya
4. Perpotongan antar diagonalnya membentuk sudut siku-siku

Baca juga Persegi Panjang.

Rumus Keliling Persegi

Semua jenis bangun datar pasti memiliki keliling, tidak terkecuali bangun datar persegi.

Menghitung keliling persegi dapat dengan cara mengalikan 4 sisinya. Hal ini dikarenakan keliling persegi merupakan penjumlahan keempat sisinya yang sama panjang.

Sehingga rumus keliling persegi adalah

Rumus Keliling Persegi

Keliling = sisi + sisi + sisi + sisi

atau

Keliling = 4 x panjang sisi persegi

Rumus Luas Persegi

Selain keliling, bangun datar persegi juga memiliki luasan, dimana luasan persegi dihitung dengan menguadratkan panjang sisinya.

Sehingga rumus untuk luas persegi adalah

Rumus Luas Persegi

Luas = (panjang sisi persegi)²

Baca juga Belah Ketupat.

Contoh Soal Persegi

1. Jika Ani ingin memasang ubin pada lantai rumahnya yang memiliki luas 64 m² dan ubin tersebut berbentuk persegi dengan panjang sisinya 40cm. Berapa jumlah ubin yang diperlukan oleh Ani?

Pembahasan

Luas ubin = 40 cm x 40 cm = 1600 cm²

Banyaknya ubin yang diperlukan 

Jadi, banyaknya ubin yang diperlukan Ani untuk membuat lantai adalah  400 buah.

2. Denah rumah Budi terlihat seperti gambar berikut

Jika rumah Budi akan dipasang lampu natal mengelilingi rumahnya, jika Budi sudah membeli lampu natal sepanjang 50 m, maka apakah lampu natal yang  dibeli oleh Budi cukup, sisa, atau kurang? Jika sisa atau kurang, berapakah panjang sisa atau kurangnya tersebut?

Pembahasan

Keliling rumah Budi = 4 x 12 m = 48 m

Karena keliling rumah Budi lebih kecil daripada panjang lampu natal yang dibeli Budi, maka lampu natal yang dibeli masih memiliki sisa.

Sisa lampu natal  = 50 m – 48 m = 2 m

Jadi, lampu natal yang dibeli oleh Budi masih memiliki sisa, sisa lampu natal milik Budi adalah 2 meter.

Demikian pembahasan tentang persegi. Semoga bermanfaat.

Read More